Os grafos, em que os objetos e as suas relações são representados como nós (ou vértices) e arestas (ou ligações) entre pares de nós, são omnipresentes na computação e na aprendizagem automática (ML). Por exemplo, as redes sociais, as redes rodoviárias e a estrutura e interações moleculares são todos domínios em que os conjuntos de dados subjacentes têm uma estrutura gráfica natural. O ML pode ser utilizado para aprender as propriedades de nós, arestas ou grafos inteiros.

Uma abordagem comum para a aprendizagem em grafos são as redes neurais de grafos (GNNs), que operam em dados de grafos aplicando uma transformação otimizável em nós, arestas e atributos globais. A classe mais típica de GNNs opera por meio de uma estrutura de message-passing, em que cada camada agrega a representação de um nó com as de seus vizinhos imediatos.

Recentemente, os modelos de transformadores de grafos surgiram como uma alternativa popular aos GNNs de passagem de mensagens. Estes modelos baseiam-se no sucesso das arquiteturas Transformadoras no processamento de linguagem natural (NLP), adaptando-as a dados estruturados em grafos. O mecanismo de atenção nos transformadores de grafos pode ser modelado por um grafo de interação, em que as arestas representam pares de nós que se entendem mutuamente. Ao contrário das arquiteturas de passagem de mensagens, os transformadores de grafos têm um grafo de interação que é separado do grafo de entrada. O grafo de interação típico é um grafo completo, o que significa um mecanismo de atenção plena  que modela as interações diretas entre todos os pares de nós. No entanto, isto cria estrangulamentos computacionais e de memória quadráticos que limitam a aplicabilidade dos transformadores de grafos a conjuntos de dados em pequenos grafos com, no máximo, alguns milhares de nós. Tornar os transformadores de grafos escaláveis tem sido considerado uma das direções de investigação mais importantes neste campo (ver o primeiro problema em aberto aqui).

Um remédio natural é usar um gráfico de interação esparso com menos arestas. Muitos transformadores esparsos e eficientes foram propostos para eliminar o gargalo quadrático para sequências, no entanto, eles geralmente não se estendem a grafos de uma maneira baseada em princípios.

Em “Exphormer: Transformadores esparsos para grafos“, apresentado no ICML 2023, abordamos o desafio da escalabilidade introduzindo uma estrutura de atenção esparsa para transformadores que é projetada especificamente para dados de grafos. A estrutura Exphormer faz uso de gráficos expansores, uma ferramenta poderosa da teoria dos gráficos espectrais, e é capaz de obter resultados empíricos fortes em uma ampla variedade de conjuntos de dados. Nossa implementação do Exphormer está agora disponível no GitHub.

Grafos de expansão

Uma ideia chave no coração do Exphormer é o uso de gráficos expansores, que são grafos esparsos mas bem conectados que têm algumas propriedades úteis – 1) a representação matricial dos grafos tem propriedades algébricas lineares semelhantes às de um grafo completo, e 2) eles exibem uma mistura rápida de passeios aleatórios, ou seja, um pequeno número de passos num passeio aleatório a partir de qualquer nó inicial é suficiente para garantir a convergência para uma distribuição “estável” nos nós do grafo. Os expansores têm encontrado aplicações em diversas áreas, tais como algoritmos, pseudo-aleatoriedade, teoria da complexidade e códigos de correção de erros.

Uma classe comum de grafos expansores são os expansores d-regulares, nos quais existem arestas a partir de cada nó (ou seja, cada nó tem grau de). A qualidade de um grafo expansor é medida pelo seu défice espectral, uma propriedade algébrica da sua matriz de adjacência (uma representação matricial do grafo em que as linhas e colunas são indexadas por nós e as entradas indicam se os pares de nós estão ligados por uma aresta). Aqueles que maximizam a lacuna espectral são conhecidos como gráficos de Ramanujan – eles atingem uma lacuna de d – 2*√(d-1), que é essencialmente a melhor possível entre gráficos regulares. Várias construções determinísticas e aleatórias de grafos de Ramanujan foram propostas ao longo dos anos para vários valores de d. Usamos uma construção de expansor aleatório de Friedman, que produz grafos quase-Ramanujan.

O Exphormer substitui o gráfico de interação denso e totalmente conectado de um Transformer padrão por arestas de um gráfico expansor regular esparso de. Intuitivamente, a aproximação espectral e as propriedades de mistura de um grafo expansor permitem que nós distantes se comuniquem uns com os outros depois que uma pessoa empilha várias camadas de atenção em uma arquitetura de transformador de grafo, mesmo que os nós não possam atender uns aos outros diretamente. Além disso, ao garantir que d é constante (independente do tamanho do número de nós), obtemos um número linear de arestas no gráfico de interação resultante.

Exphormer: Construção de um grafo de interação esparso

O Exphormer combina arestas de expansão com o gráfico de entrada e nós virtuais. Mais especificamente, o mecanismo de atenção esparsa do Exphormer constrói um gráfico de interação que consiste em três tipos de arestas:

• Arestas do grafo de entrada (atenção local)
• Arestas de um grafo expansor de grau constante (atenção do expansor)
• Arestas de cada nó para um pequeno conjunto de nós virtuais (atenção global)

Cada componente serve um objetivo específico: as arestas do grafo de entrada retêm a tendência indutiva da estrutura do grafo de entrada (que normalmente se perde num módulo de atenção totalmente ligado). Entretanto, as arestas de expansão permitem uma boa conectividade global e propriedades de mistura de passeios aleatórios (que se aproximam espectralmente do grafo completo com muito menos arestas). Finalmente, os nós virtuais servem como “sumidouros de memória” globais que podem comunicar diretamente com cada nó. Embora isso resulte em arestas adicionais de cada nó virtual igual ao número de nós no gráfico de entrada, o gráfico resultante ainda é esparso. O grau do gráfico expansor e o número de nós virtuais são hiperparâmetros a ajustar para melhorar as métricas de qualidade.

Além disso, como usamos um grafo expansor de grau constante e um pequeno número constante de nós virtuais para a atenção global, o mecanismo de atenção esparso resultante é linear no tamanho do grafo de entrada original, ou seja, modela um número de interacções directas da ordem do número total de nós e arestas.

Além disso, mostramos que o Exphormer é tão expressivo quanto o transformador denso e obedece a propriedades universais de aproximação. Em particular, quando o gráfico de atenção esparso do Exphormer é aumentado com auto-loops (arestas que conectam um nó a si mesmo), ele pode aproximar universalmente funções contínuas [1, 2].

Relação com transformadores esparsos para sequências

O grafo de Erdős-Rényi em n nós, G(n, p), que conecta cada par de nós independentemente com probabilidade p, também funciona como um grafo expansor para p adequadamente alto. No entanto, um número superlinear de arestas (Ω(n log n)) é necessário para garantir que um grafo Erdős-Rényi seja conectado, quanto mais um bom expansor. Por outro lado, os expansores usados no Exphormer têm apenas um linear número de arestas.

Resultados experimentais

Trabalhos anteriores mostraram o uso de modelos baseados em transformador de grafo completo em conjuntos de dados com grafos de tamanho de até 5.000 nós. Para avaliar o desempenho do Exphormer, baseamo-nos na célebre estrutura GraphGPS [3], que combina passagem de mensagens e transformadores de grafos e atinge o desempenho de ponta em vários conjuntos de dados. Mostramos que a substituição da atenção densa pelo Exphormer para o componente de atenção ao grafo na estrutura GraphGPS permite obter modelos com desempenho comparável ou melhor, muitas vezes com menos parâmetros treináveis.

Além disso, o Exphormer permite, nomeadamente, que as arquitecturas de transformação de grafos sejam dimensionadas muito para além dos limites habituais de tamanho dos grafos acima referidos. O Exphormer pode escalar até conjuntos de dados de grafos com mais de 10.000 nós, como o conjunto de dados Coauthor, e até mesmo além de grafos maiores, como o conhecido conjunto de dadosogbn-arxiv, uma rede de citações, que consiste em 170K nós e 1,1 milhão de arestas.

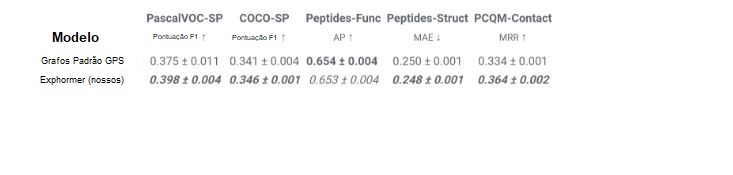
Finalmente, observamos que o Exphormer, que cria um gráfico de sobreposição de pequeno diâmetro por meio de expansores, exibe a capacidade de aprender efetivamente dependências de longo alcance. O Long Range Graph Benchmark é um conjunto de cinco conjuntos de dados de aprendizagem de gráficos concebidos para medir a capacidade dos modelos para capturar interações de longo alcance. Os resultados mostram que os modelos baseados em Exphormer superam os modelos GraphGPS padrão (que eram anteriormente o estado da arte em quatro dos cinco conjuntos de dados no momento da publicação).

Conclusão

Os transformadores de grafos surgiram como uma arquitetura importante para o ML que adapta os transformadores baseados em sequências de grande sucesso utilizados na PNL a dados estruturados em grafos. A escalabilidade tem, no entanto, provado ser um grande desafio para permitir o uso de transformadores de grafos em conjuntos de dados com grafos grandes. Neste post, apresentamos o Exphormer, uma estrutura de atenção esparsa que usa gráficos expansores para melhorar a escalabilidade dos transformadores de gráficos. O Exphormer tem propriedades teóricas importantes e exibe um forte desempenho empírico, particularmente em conjuntos de dados onde é crucial aprender dependências de longo alcance. Para mais informações, apontamos o leitor para uma breve apresentação vídeo do ICML 2023.

Agradecimentos

Agradecemos aos nossos colaboradores de investigação Hamed Shirzad e Danica J. Sutherland da Universidade de British Columbia, bem como a Ali Kemal Sinop da Google Research. Agradecimentos especiais a Tom Small pela criação da animação utilizada neste post.

Publicado por Ameya Velingker, Cientista investigador, Google Research, e Balaji Venkatachalam, Engenheiro de software, Google